効用価値説
更新日:
「全ての価値は労働価値の合計によって表しうる」というのが「労働価値説」によるモノの値段の説明であった。
確かに全ての財やサービスの価格は(原材料の価格の合計)+(投入された労働量)=(モノの値段)という形で表しうるし、原材料だって労働の成果であると考えることができる。
だから、財やサービスの価値は労働価値の総計であるといえる。
これを数式で表せば、Xjを各労働者の労働投入量、ajをその労働者の労働生産性(係数)として
P(モノの価格)=a0 + a1・X1 + a2・X2 + a3・X3 + … + an・Xn
と表しうる、、、と言うことである。
だがしかし、いくら綿密に計算して労働価値を積み上げて行ったとしても、実際のモノの値段は労働価値の単純合計とは一致しない。
これを数式で表せば(さっきの式の逆であるが)すなわち
a0 + a1・X1 + a2・X2 + a3・X3 … an・Xn ≠P(モノの価格)
となる。
一番目の式と二番目の式は同じ式のはずなのに、なぜ片方は等号で結ぶことができ、もう一方は等号では結べないのか? というと、実はこれは「時刻」が異なるのだと考えるとわかりやすい。
つまり「過去に価格Pで売れたモノ」の値段は、それを製造した各生産段階の労働投入量に分解してその和として表すことができる。
だが「これから売ろうとしている同じ商品」が、次に同じ値段Pで売れるとは限らない。
需給バランスによって高く売れたり、あるいはもっと安くしか売れなかったりするし、また商品の寿命(賞味期限など)が迫ると安くたたき売られたりする。
我々の経験上そういうことはよくあるが、だがしかし、同じ努力をして作った同じ商品が、なぜ同じ値段で売れないのであろうか? そこに実は「消費者の論理」というモノがあるのである。
たとえば仕事やトレーニングの後ビールを好んで飲む人間にとって、その一杯目や二杯目のビールはとても美味いものである。
だからこのビールを飲むためにわざわざ酒場まで出かけ、ビールを飲む。
この時このビールを飲むために支払う費用は大きくても納得する。
一杯500円でも700円でもお客は対価を支払う。
だがしかし同じビールでも十杯目二十杯目ともなると、一杯目や二杯目ほどの満足は得られない。
満足が得られないなら、それに支払う対価(支払っても良いと考える金額)も下がってくる。
飲み屋でも、店に入った最初の一時間くらいは何だかんだとオーダーが出されるが、そのあとは店員さんが注文を取りに来ても誰も何も頼まなくなる。
そんな感じでそれを買う人間が満足した後(需要が充足した後)は、同じ商品に対してより安い対価しか支払われなくなる。
支払う金より受け取る価値が小さくなれば、もうその商品を買う動機は失われる。
そう言う風にモノの値段はそのモノが買い手に与える「効用(ユーティリティ)」によって決まるのだ、というのが「効用価値説」なのである。
労働価値説は生産者や労働者、つまり売り手側の論理であり、一方効用価値説は逆に消費者の立場から考えた消費者側の論理だと言える。
スタディサプリENGLISH
TOEIC 特訓コース
取引がモノの値段を決める!
労働価値説が正しいのか、それとも効用価値説が正しいのか、、そういう議論がしばらく続いた。
だが財やサービスは取引によって、生産者から消費者の手に移るものである。
すなわち「モノを売りたい生産者」と「モノを買いたい消費者」が市場で相対し、「1,000円で買ってくれ」「いや500円なら買う」といった具合に交渉しあって、それに合意に達すればその財やサービスの所有権が移動するのである。
だからある商品を売りたい者と売却条件、その商品を買いたい者と購入条件が「マッチ(一致)」する金額にモノの値段は決まる、、、、、という説に落ち着くこととなった。
当たり前と言えば当たり前の結論であるが、学問というのはそうして当たり前の結論を出すにも四苦八苦するのである。
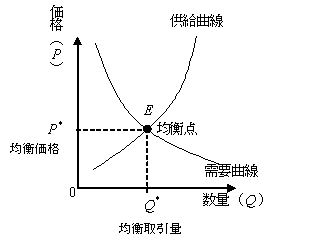
そうして例の「需要曲線」と「供給曲線」の交点が商品の価格と供給量を示すという、グラフによる説明が行われるようになった。
1)需要関数(デマンド・カーブ)
消費者は商品の価格Pとそれを買うことによって得られる満足(つまり効用)とを天秤に掛けて、満足の方が大きい場合にその商品を買う。
この時その商品の価格Pを縦軸に取り、消費量(販売量)Qを横軸に取るとすると、商品価格Pが高いときはどうしてもそれが欲しいような人しか買わないので商品の消費量(販売量)Qは0に近くなる。
そして逆に商品価格Pが安くなれば「これ前から欲しかったんだ」という感じでそれを買う人間が増え、消費量Qは0から遠くになる。
この関係をドンドンプロットしていって曲線を描いたモノがつまり「需要曲線」である。
需要関数は大勢の売り手と大勢の買い手との間の取引では、基本的に下図のような、右下がりのなだらかな曲線となる(もちろんこれは概念的なモデルであるが)。
2)供給関数(サプライ・カーブ)
では取引のもう一方である売り手(生産者)はどのようにモノを作ったり売ったりするのか? というのをグラフにしたのが供給曲線である。
売り手はある商品が高く売れるのならば、それを作って売ろうと考えるだろう。
たとえば日本では麦の自給率が低く米の自給率が高いのだ。
しかし、それは麦を作るより米を作った方が格段に良い収入になるからである。
高く売れるのなら、少々分の悪い土地でも米を作ってやっていける。
だから日本の穀物農家は(余っているというのに)米ばかり作ろうとする。
だがしかし、もし米の価格が低くなれば分の悪い土地で米を生産している農家は立ち行かなくなる。
米を作らず田んぼにビニール・ハウスを建てて、ナスやキュウリやトマトやイチゴを作ったり、あるいは出稼ぎに出た方が稼ぎになる。
すなわち米の価格Pが高ければ、米の供給量は大きくなる。
そして逆に価格Pが低ければ、米の供給量は小さくなる。
、、、という関係になる。
3)マッチング(市場均衡)
政治的に補助金やその他の費用(取引費用)などがない場合、買い手が支払う対価pと売り手が受け取る対価pは等価である。
だから1)と2)のグラフの縦軸は共用できる。
そして同じく政治的な介入や受け渡しロスなどがない場合、売り手が売り渡す販売量qと買い手が購入する購入量qも同じ量である。
だから1)と2)のグラフの横軸も共用できる。
そういうわけで1)と2)のグラフを重ねることができる。
だから、この二つの曲線(需要曲線と供給曲線)の交点が「取り引きされる価格」と「取り引きされる量」ということになる。
需要供給曲線
こうしてモノの値段を決めるのは「労働価値」か「効用価値」かという論争は、余り意味のないモノとなったのである。
(つづく)
今回の・・・
恥ずかしながらボクは、農学部の経済学コースに進学して数ヶ月はこの市場均衡のグラフの意味がよく理解できませんでした。
というのも生産量Qは、価格Pの関数として捉えることができる。
だから、縦軸がQ(数学のグラフの場合のy軸)で横軸がP(x軸)の方が理解しやすかったからです。
だからこの描き方になれるまでは、自分で勝手にその様にグラフを描いて理解していました。
ただ色々なグラフ(たとえばバット・ダイヤグラムとか)を描く場合には、それでは説明しにくくなります。
だから次第に普通にグラフを描くようになりましたが、経済学のグラフというのは常に縦横自由自在に読めないと困るようなグラフが多いのも確かです。
面倒やね、、、、